Entanglement of Quantum States
By Aaron, Neil
External mentor: Tianci Zhou, Virginia Tech Center for Quantum Information Science and Engineering
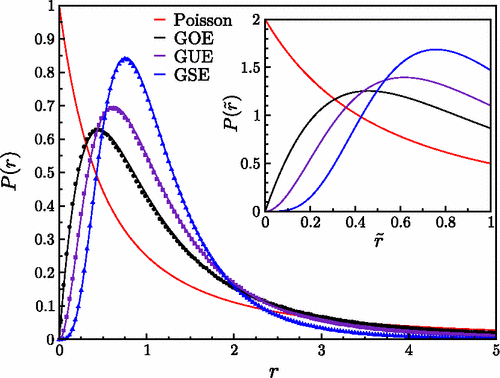
The proposed research aims to explore the level statistics of quantum Hamiltonians. In this case, the energy levels are the eigenvalues of the Hamiltonian operators. Recently, we have seen such statistics applied to quantum circuits. We aim to study the properties of a quantum system using its eigenvalues via random matrix level statistics. In addition, we also aim to look at the entanglement of eigenstates in quantum scars. Eigenstates typically have volume-law entanglement to be consistent with thermalization. Quantum scars, however, are a special class of quantum systems, a subset of which can have area-law entanglement (entanglement scales with area, not volume; low entanglement), allowing them to periodically revive the wave function rather than trend towards thermal equilibrium.
The intellectual merit of this research lies in the potential of our work to develop our understanding of entanglement in many-body systems. For Project 1, we will build on the description of random matrix theory (RMT) of quantum chaos that predicts that the energy levels of chaotic Hamiltonians exhibit level repulsion and follow universal gap statistics. Project 2 will extend this to quantum circuits; we will explore whether the circuit spectra obey the same behavior to see if we can make a connection to quantum chaos. Conventional eigenstate thermalization predicts volume-law entanglement across the spectrum. Recent work has contradicted this by revealing quantum scar states with area-law (low) entanglement, causing dynamical revivals. By characterizing the entanglement structure of eigenstates in quantum scars, we aim to clarify when and how scars emerge.
Our results will guide us to design circuits that can emulate chaotic thermalization behavior or avoid it, based on use case. Our study of quantum scars may also lead us to develop protocols that exploit non-thermal states to enhance the lifetimes of quantum memory. Our work will generate datasets of spectra and gap ratios that can be utilized for machine learning approaches to state classification, or for educational purposes.
Files and Resources
Files are coming soon!
Photo Gallery